1-Görme olayının ilk doğru açıklamasını yapmıştır.
2-Gözün fiziksel özellikleri.
3-İki gözün aynı cismi tek olarak görme olayının açıklanması.
4-Küresel ve parabolik aynalar, küresel aberasyon, cisimlerin ağırlık merkezi problemleri, izoperimetrl, trisseksiyon meselesi, diyoptri konuları.
5-Işığın; hava, su ve değişik ortamlardan geçerken kırılma olayları.
6-Kırılma açıları arasındaki oranın sabit olmadığı.
7-Işığın yansıma olayının açıklanması ve ışığın geliş açısı ile yansıma açısı arasındaki oran hakkında bilgiler.
8-Küçük açılar altında gelen ışınların kırılma kanunları (kepler’e atfedilir.)
9-Mercek, prizma, aynaların çeşitleri ve fiziksel özellikleri
10-Güneş ışınlarının fiziksel özellikleri.
11-Güneş ile Ay’ın ufuk noktasına yaklaşınca daha büyük görülme nedenlerinin açıklanması.
12- Güneş’in, ufuk noktasında görülmeden önce ve battıktan sonra, ufuk düzleminin ancak 19 derece aşağıda bir noktaya gelince “alaca karanlığın” başladığını açıklamıştır. Böylece tan olayı kavramına yeni boyutlar kazandırmıştır.
13-Küresel astronomi ile ilgili bilgiler.
14-Atmosfer basıncı ve bu basınç değerinin atmosfer yüksekliği ile değişimi.
15-Atmosfer basıncının yıldızlardan gelen ışınlar üzerine etkileri.
16-Atmosfer yoğunluğunun, ışığın kırılması ile doğru orantılı olduğu ve atmosfer yoğunluk değerinin yükseklik ile değişimi.
17-Yerküre (dünya) atmosfer tabakasının 15 km. civarında olabileceği.
18-Ay’ın hâle durumunun açıklanması.
19-Gökkuşağı (alâim-i semâ) olayının açıklanması.
20-Fizikte geniş uygulama alanı olan “karanlık oda” olayı ile ilgili bilgiler. (levi ben gerson’a ‘1288-1344’ atfedilir.)
21-Ölçü geometrisi, elips ve daire terkibi.
22-Cebirle çözüldüğü vakit 4. dereceden bir problem haline dönüşe bilen “bilardo veya küresel ayna probleminin” geometrik olarak çözümü konularında temel bilgiler ilk defa açıklanmıştır.
...Copyright (C) Gerçek Bilim kaynağını göstermeden paylaşmak ve yayınlamak yasaktır, https://www.gercekbilim.com/fotograf-makinesinin-babasi-ibn-i-heysem/ .
‘Göz görme organımızdır.’ Bu tek cümleye mutlaka ‘doğru’ ya da ‘yanlış’ dememiz gerekiyorsa, ben bu cevaba ‘yanlış’ diyorum. Çünkü görmemizi nihai anlamda sağlayan organımız beyindir ve göz adeta görmemize yardımcı ana organımızdır.
Gözün Yapısı ve Görevi Nedir? Biliyor musunuz?
Göz ‘kendisine gelen ışık enerjisini elektro-kimyasal enerjiye çeviren bir aygıttır’ ifadesi gözün yaptığı işi doğru tanımlayan bir ifadedir. Bunun için gözün önce yapısına sonra ise nasıl çalıştığına göz atalım.
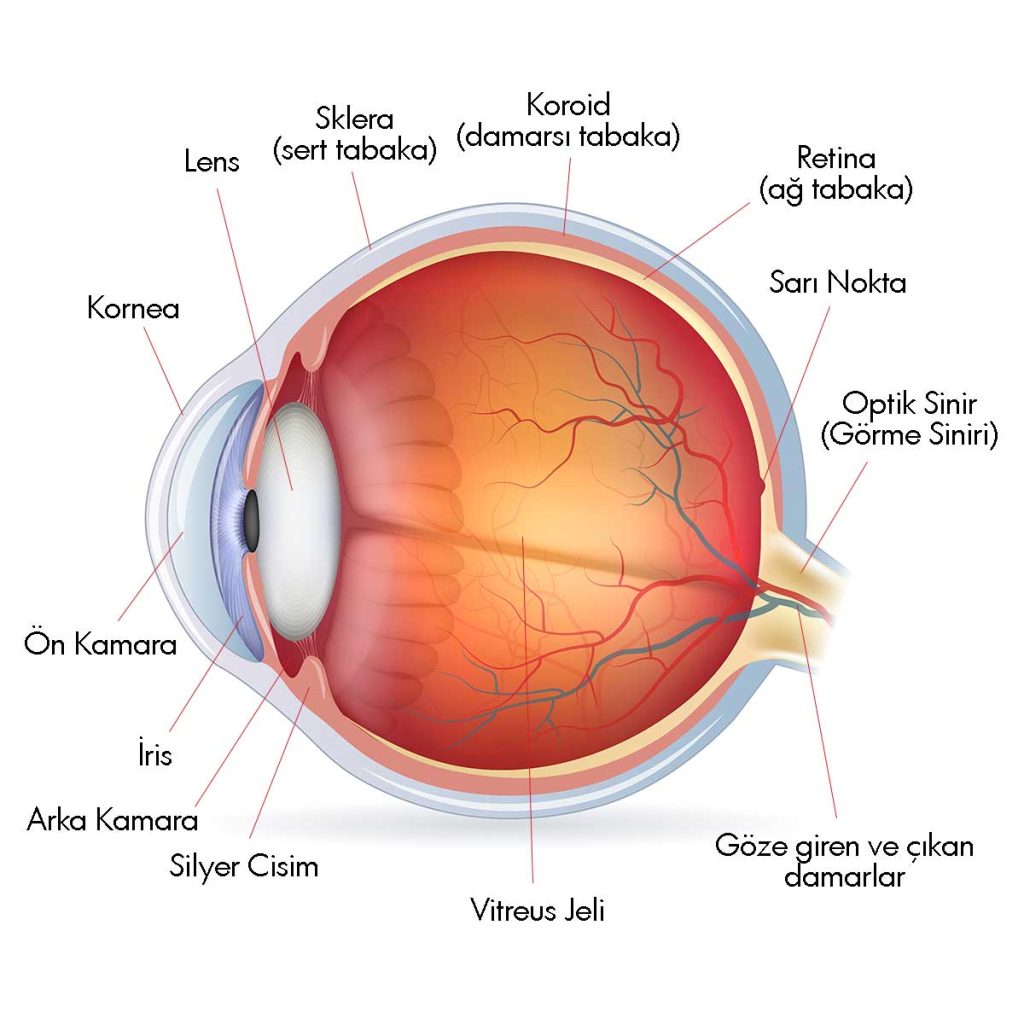
Gözün Dış Duvarı
Gözün dış duvarı dışarıdan iç kısma doğru 3 katmandan oluşmaktadır.
- Kornea (Saydam Tabaka) ve Sklera (Sert Tabaka)
- Damarsal Tabaka (Koroid)
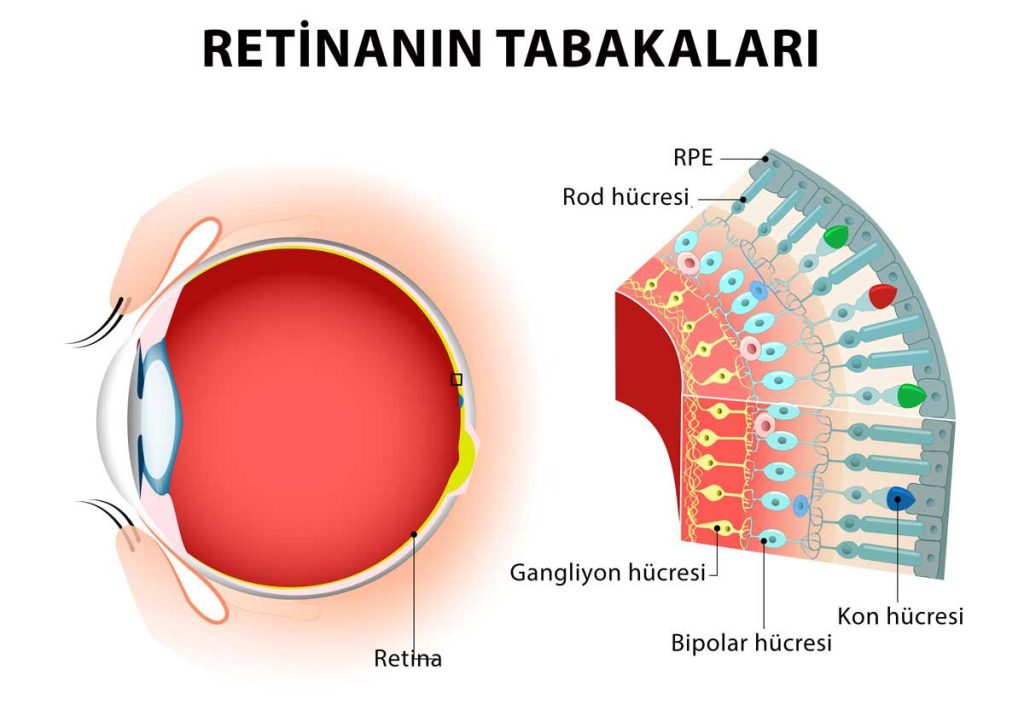
- Retina (Ağ tabaka)
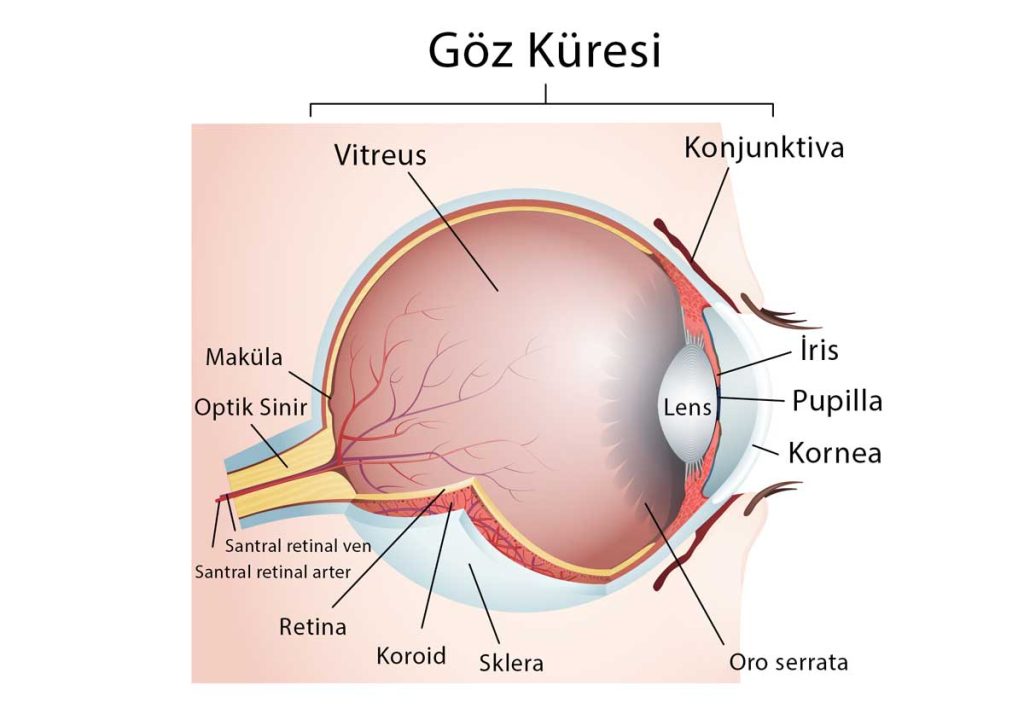
Retinada yırtıklar oluşabilir. Bunun yanında arka üveit adı verilen göz içi iltihabi durumlar retinayı etkileyebilir. Şeker hastalığına ve sarı nokta hastalığına bağlı retinada hasarlar ortaya çıkabilir.
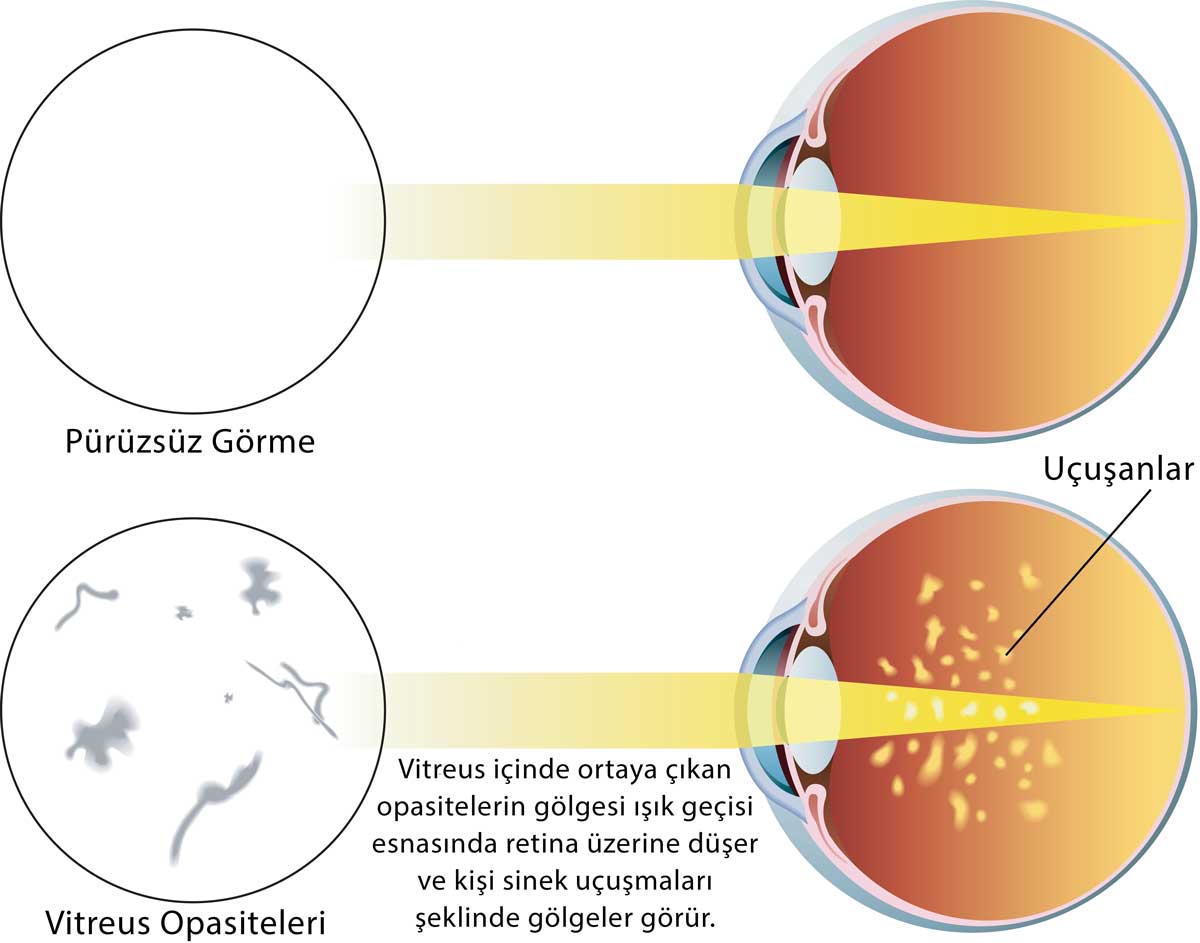
Bu opasiteleri gözümüzün önünde sinek uçuşmaları tarzında gözlemleriz.
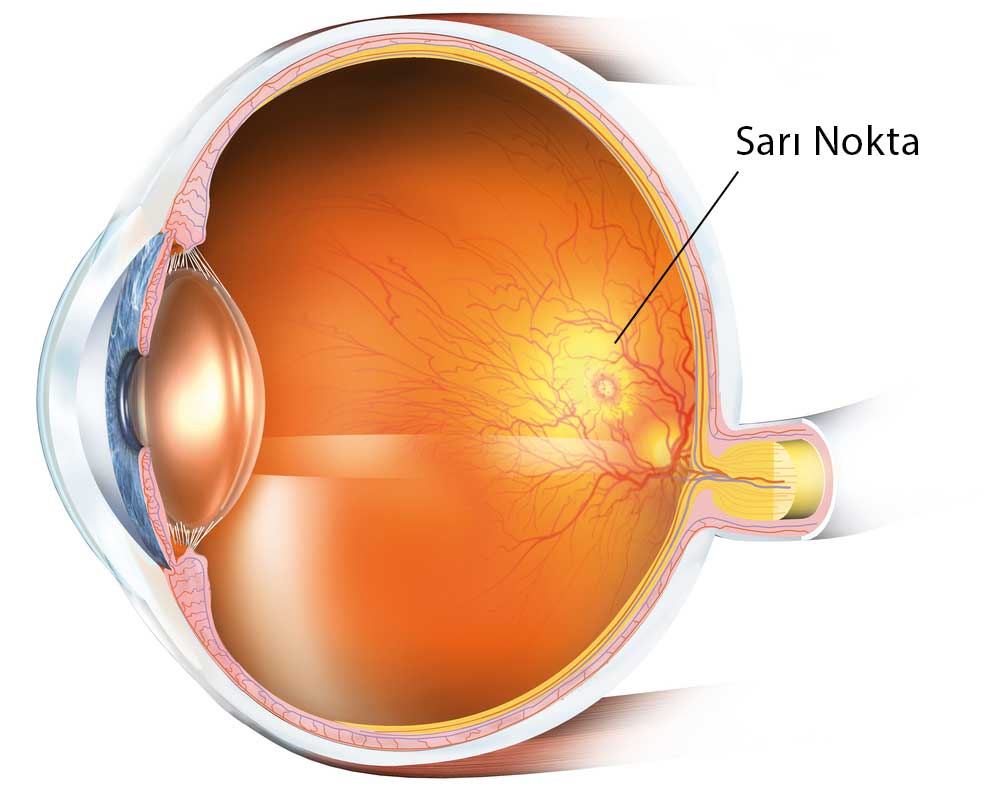
Görme Siniri
Görme Siniri retinadaki ışık enerjisini elektro-kimyasal enerjiye çeviren yaklaşık 1.200.000 adet sinir lifinin birleşmesi sonrasında ortaya çıkmaktadır. Görme siniri (optik sinir) retinada ortaya çıkan elektro-kimyasal uyarıyı beyimizin arka kısımlarında bulunan görmeden sorumlu alana iletmektedir. Beynin arka kısmında olan görme merkezi optik sinir lifleri ile kendisine gelen elektro-kimyasal iletiyi gördüğümüz görüntüye çevirmektedir.
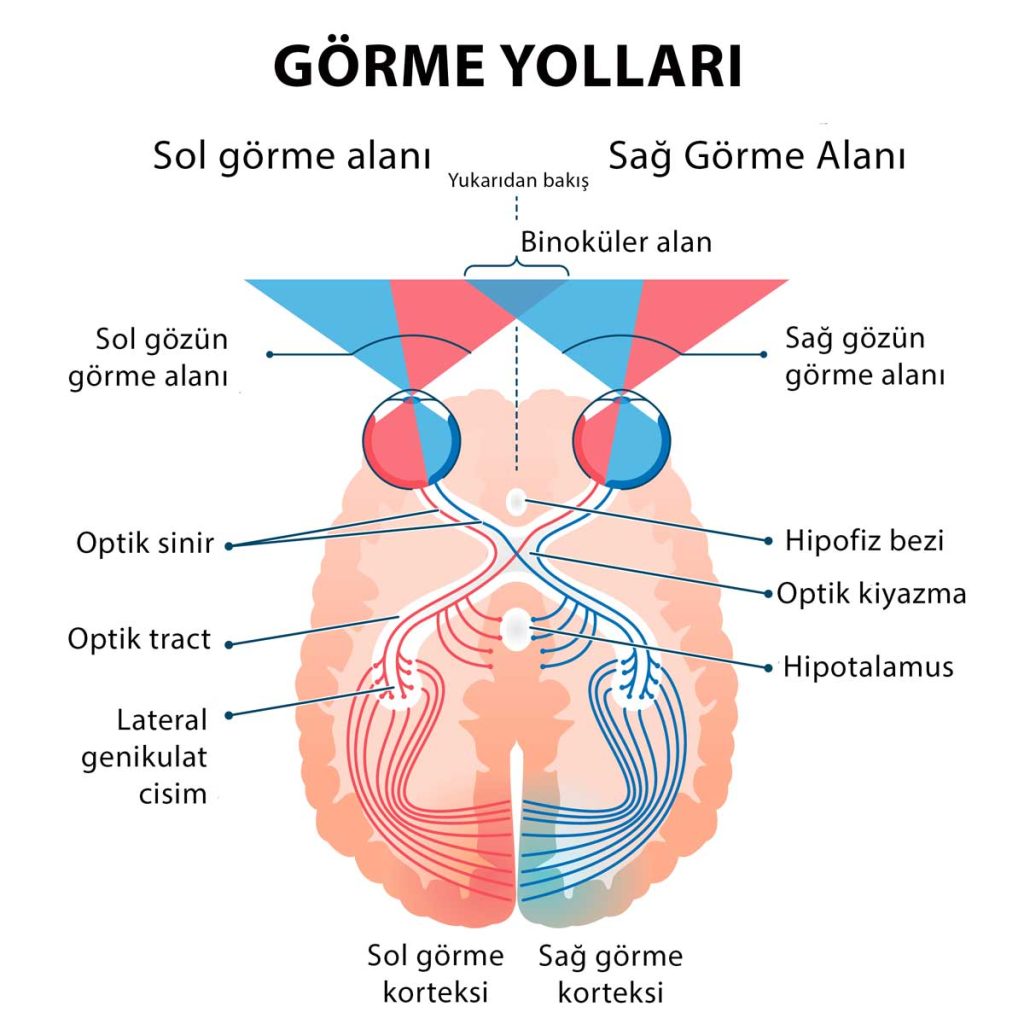
Beyin Anatomisi
OKSİPİTAL LOB: Beynin arka kısmında, ensenin üzerinde yer alır. Görme merkezidir. Görmenin anlaşılması ve eski bilgilerle birleştirilmesi bu bölgede yapılır. Bu bölgenin hasarları görme alanında defektlere yol açar.
2. Optik Sinir: Görme
3. Okulomotor Sinir: Göz hareketleri
4. Troklear Sinir: Göz hareketleri
6. Abdusens Siniri: Göz hareketleri
Prof. Dr. Selçuk Peker

Cisimlerin biçimlerini ışık yardımı ile görürüz. Işığın yapısı ile ilgili Newton'un tanecik teorisi ve Huygens'in dalga teorisi 1923 lü yıllara kadar birbirinden ayrı iki teori olarak gelişmiştir. Fakat 1923'te De Broglie'nin madde dalgalarına zemin hazırlayan açıklamaları ile bu iki teori birleşmiştir.
Gelinen son nokta ise ışığın hem dalga hem de tanecik özelliğine sahip olduğudur.
Işık olayı üçe ayrılır:
- Dalga olarak davranması
- Tanecik olarak davranması
- Hem dalga hem de tanecik olarak davranması
Işığın Dalga Olarak Davranması: Kırınım, Girişim, Işığın kırılırken bir kısmının yansıması ve polarizasyon olayı ışığın dalga olarak davranmasına verebileceğimiz örneklerdir.
Işığın Tanecik Olarak Davranması: Işık basıncı, Fotoelektrik olay ve Compton olayı ışığın tanecik olarak davranmasına verebileceğimiz örneklerdendir.
Işığın Hem Dalga Hem de Tanecik Olarak Davranması: Doğrusal olarak yayılma, Yansıma, Kırılma, Işık akısı, Gölge oluşması, Beyaz ışığın renklere ayrılması, Işığın birbiri içerisinden geçmesi ışığın hem dalga hem de tanecik olarak davranmasına verebileceğimiz örneklerdir.
Albert Einstein, kuantize olanın sadece ışığın yayılması değil, ışığın kendisi olduğunu öne sürdü. Einstein’a göre ışık küçük parçacıklardan (sonunda foton adını aldı) oluşur ve bir grup foton bir araya geldiğinde bir dalga gibi davranır. Bu dalga-parçacık ikiliği, radikal olmasına rağmen, bir dizi deney ve gözlemi açıklayabilir.
⚠️ Einstein’ın ünlü E= Mc^2 denklemini duymuştur . Bu kısmen şu anlama geliyor, bir parçacığı oluşturmak için kütlesine orantılı enerjiler gerekir. Küçük kütleye sahip nötrinoları oluşturmak kolaydır, elektronlar için daha büyük enerjiler gerekirken, Higgs bozonunu oluşturmak için çok büyük enerjiler gerekir.
peki desen nasıl? çok ilginç. aydınlık - karanlık - aydınlık - karanlık diye tekrar eden ince saçaklar. açıklaması ne? vallahi efendim ışık dalgaymış meğer. eğer ışığın birinci delikten perde üzerindeki x noktasına kadar gittiği mesafe ile ikinci delikten perde üzerindeki x noktasına kadar gittiği mesafe dalga boyunun tam katıysa, o zaman bu iki dalgayı tepe+tepe veya çukur+çukur diye topluyoruz. sonuç o noktada iki kat parlak bir ışık.
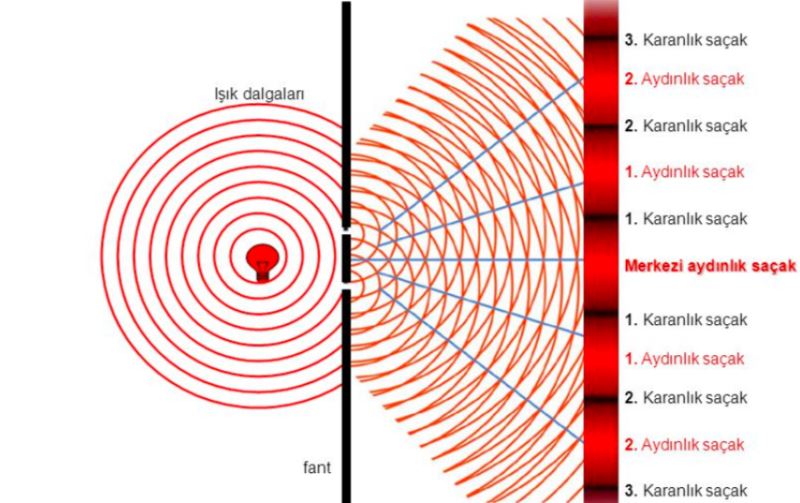
halbuki başka bir y noktasında bu mesafeler farkı, dalga boyunun buçuklu katıysa o zaman tepe+çukur veya çukur+tepe diye topluyoruz. sonuç sıfır. o noktada hiç ışık görmüyoruz. bu fenomenin adı "girişim".
bu deney, ışığın dalga davranışı sergilediğini ortaya çıkartmıştı eskiden. buna benzeyen, ama çok daha enteresan olan bir deney biliyorum ama ben: de broglie deneyi. yani dalga olduğu zannedilmeyen şeylerin bile girişim yapması. mesela elektron.
⚠️Su dalgalarında, periyodik olarak değişen şey su yüksekliğidir. Ses dalgalarında ise bu, basınçtır. Işıkta ise, periyodik olarak değişen şey, elektrik ve manyetik alandır.
Âl-i İmrân / 190. Ayet
Şüphesiz göklerin ve yerin yaratılışında, gece ile gündüzün birbiri ardınca gelip gidişinde akl-ı selim sahipleri için pek çok delil ve ibretler vardır.
En'âm / 13. Ayet
Gecenin karanlığı, gündüzün aydınlığı içinde barınan her şey O’nundur.
Fraktal tam olarak nedir?
Fraktalın tek bir matematiksel tanımı yok. Fraktalın ne olduğunu anlamak için en iyi yol, bir ağaç düşünmektir.
bir ağaç parçalara ayrılabilir ve her parça ağacın bütününe neredeyse tıpatıp benzer. Son çözümlemede, fraktal yöntemler, kendine benzer (İng. self-similar) parçalardan oluşan doğal ya da yapay her "sistem"i analiz etmek için kullanılabilir.
Apayrı düşünceleri görsel olarak birbirine bağladınız.
Benim bilimsel yaşantımın öyküsü bu: Araştırırken resimlere bakarım, bakarım, bakarım ve onlarla oynarım. Bir resme bir bakış atmak, bilimsel bir aygıttan veri okumak gibidir. Bir kez yapmak asla yeterli olmaz. Büyük bir biyolog ve felsefeci olan Almanya doğumlu bir arkadaşım, bilimdeki ilerlemenin resimleri mümkün olduğunca elemekle ilgili olduğunu ortaya atacak kadar ileri gitmişti.Matematik kusursuzdu çünkü resimlerden bütünüyle kurtuluyordu- en temel ders kitaplarında bile. Ben resimleri geri koydum. Bu durum, meslektaşlarımın çoğu tarafından düşmanca karşılandı. O zamana kıyasla, resimlere olan karşıtlık zayıfladı. Bunun nedeni de olağanüstü verimlilikte olmaları ve insanların sürekli değişmeleri...
Peki, bu çeşit bir aracın kendi tehlikeleri yok mu?
Resimler yol gösterebildikleri gibi insanı aldatabilirler de. Beyin, desen olarak kavradıklarını öne çıkarır; bunu yanlışlayan enformasyonu ise göz ardı eder. İnsan doğası, dünyada düzen ve hiyerarşi görmek için yanıp tutuşur. Bulamadığı yerde de onu icat eder.
Bu düşünce biçimi neden daha yaygın değil?
Bilimde resimlere gereken değer verilmiyor. Onlara güvenilmiyor. Yani kısmen Fransız matematikçiler Lagrange ile Laplace'ın (onlar tüm mantıksal düşünceyi net formüllere ve dikkatle seçilmiş sözcüklere indirgemek için titizlikle çalışmıştı) 200 yıllık mirasından dolayı, dağınık diyagramlar hep kuşkuyla karşılanmıştır. Onların itici gücü, sanıyorum kısmen teknolojikti: O zamanlar çizimler kesinlikten uzak ve masraflıydı; insan elinin ürünüydüler. Fakat bizim yaşadığımız çağda, bilgisayarlar bu durumu tamamen değiştirdi.
Halk arasında, çalışmalarınız sırasında ortaya çıkan güzel fraktal resimlerden bazıları ile ünlüsünüz.
Matematik, güzel şekiller için akıl almaz derecede verimli bir kaynak. Bu şekiller bize sanatçılarla rekabet etme ayrıcalığı tanıyor. Yeni başlayanlar, bu alanda profesyonel değiller ve yarattıkları şekiller büyük ressamların tablolarıyla boy ölçüşemeyebilir. Ama çizmeyi öğreniyoruz. Bilgisayar sanatının Rembrandt veya Picasso'su henüz kendini belli etmedi. Yine de şimdiye dek gördüklerimiz cesaret verici ve belki de formüllü sanat, yeni bir sanat biçiminin başlangıcı olabilir.
Sanat matematiği çekici kılabilir mi?
Arkadaşlarımın çoğu, fraktal geometrinin en harika yanlarından birinin, eşleri ile ilişkilerini iyiye götürmesi olduğunu söyledi. Uzun süredir eşlerine uğraştıkları şeyin olağanüstü güzellikte olduğunu; muhteşem güzellikte bir teoremi, eski bir teoremin inanılmaz güzel bir kanıtını ya da bir şey hakkında harikulade güzellikte bir düşünce biçimini bulduklarını söylüyorlardı. Eşleri de başlarını sallayıp "Tabii canım" diyorlardı. Ama bir gün o eşler ellerinde resimlerle döndüler ve şöyle diyebildiler: "Gördün mü, sana söz ettiğim güzellik böyleydi..."
Fraktal sanatını böylesine özel yapan nedir?
En minimal sanatçının bir çalışmasına bakın ve alıcının birebir kopyasını yapabileceği şekilde bir mektupta o eseri betimlemeyi deneyin. Bunu sözcüklerle yapmak için aşırı derecede uzun bir tanım gerekir. Ama fraktal bir ejderhayı üreten denklem tek satırdan ibarettir. Eğer doğru entelektüel donanıma ve bilgisayar donanımına sahip birine bu denklemi verirseniz onun birebir aynısını üretebilir. Yani bu sanat, tüm sanatların en minimalidir.
Matematik ile sanatın bu şekilde etkileşimi sıradışı bir durum mu?
Matematikçiler, tüm diğer bilimcilerden ve aslında tüm diğer insanlardan farklıdır. Çünkü matematik, insanı hiçbir belirsizliği hoş görmemek üzere eğitir; bu bir gerekliliktir. Ancak biz tartışmalı olduğu kadar eski bir konuyla uğraşıyoruz: Matematiksel kavramların tüm grafik temsilleri bir sanat formudur ve ne kadar basitse o kadar iyidir. Ressam terminolojisiyle konuşmak gerekirse, buna "minimal sanat" denebilir. Bunun birazı M.C. Escher'in mirası mıdır? Öyle olmalı çünkü Escher, Fricke & Klein 1897'de kendisine hiperbolik döşemelerden esinlenme izni verme erdemine sahipti. Fraktal "yeni geometrik sanat", büyük ustaların tablolarına ya da mimarideki güzel sanatlara şaşırtıcı benzerlikler sergiliyor. Fraktal sanat çabucak kabul görebilir çünkü aslında o kadar da yabancı değil.
Eğer sanat ile bağlantı bu denli güçlü ise sanatçıların çalışmanızı dikkate alması gerekir.
Çok sayıda sanatçı, fraktalların doğasını kavrayışlarını ifade edecek bir sözcük dağarcığına sahip değil. Yine de böyle bir anlayış, çalışmalarında kolayca göze çarpıyor.
Birkaç örnek verebilir misiniz?
Fraktal olduğu kesin olan müzik yapan birkaç ekol var. Wuorinen, çalışmalarında güçlü biçimde fraktal temalar kullanıyor ama bu şekilde fraktal müzik bestelemiyor. Gyorgy Ligeti de çok iyi bir arkadaşım. Müzikte hiçbir dilin açıklayamayacağı belli bir yapı olduğuna ilişkin hisleri olduğunu söylemişti. Bunu çocuklara elden geldiğince örnekle anlatmaya çalışmak zorundaydı. Fraktallar hakkındaki kitabı ilk gördüğünde ise söz ettiği yapının fraktal yapıdan başka bir şey olmadığını fark etti ve bu onu çok etkiledi. Benim resimlerimi görene dek müziğin önemli bir yanını anlamamış olduğunu söyledi: Canının istediği gibi yapamazsın çünkü fraktal olması gerekir. Müzik ekolleri, müziğin gürültüden nasıl ayırt edileceğini asla öğretmez. Hem Wuorinen hem de Ligeti, bana gelip en sonunda müziğin neye benzediğini anladıklarını söylemişlerdi. Çünkü onlara genç yaşlarındayken bazı parçaların ayrıntılarının çok az olacağı, bazılarının ise çok ayrıntılı olacağı ve her nasılsa müziğin en başta yapması gereken şeyin küçük, orta ve büyük ayrıntıların uygun bir desenine sahip olması gerektiği öğretilmişti. Eğer Mozart'ın sonaralarından birini dinlerseniz bunu çok iyi görürsünüz: Parçalara bölünmüştür ve sürekli bir şeyler değişir. Bu basit düşünce de müziğin kabul edilebilirliği için en temel gerekliliktir.
Peki ya müziğin dışında?
Rus ressam Wassily Kandinsky, yaklaşık 0,3 m2'lik bir kağıt üzerinde çalışırken kendini filme almıştı. Bütün kağıdı ikiye ayıran bir eğri ile başladı ve daha kısa eğriler eklemeye devam etti. Film durduğunda çok daha kısa eğrilerle çalışmayı sürdürüyordu ve Kandinsky'nin resimlerine baktığımda duyduğum bir hissi doğruluyordu: Fraktallığı anlamıştı. Belki açık bir biçimde değil ama sezgisel olarak anlamıştı. Büyük ölçüde İtalya'da çalışmış olan Fransız ressam Claude Lorrain, gerçekçi olma iddiasında manzaralar çiziyordu. Ama aslında olağanüstü basitleştirilmiş ve fraktal açıdan kolayca yorumlanabilir resimlerdi. Joseph Turner'ın denizde yanan gemileri çizdiği aşırı acayip resimleri de Öklityen ve fraktal şekillere kusursuzca uyar. Eugene Delacroix, "Genç Bir Ressama Öğütler" adlı yazısında fraktallığı içgüdüsel olarak anladığını göstermiştir. Ancak o zamanlarda bunu araştıracak kimse yoktu. Bilimcilerin eksik bıraktığı, ressam ve fotoğrafçıların ise uygulayıp formalize edemediği bir görüngüyü ortaya koyma rolünü yerine getirdiğim için kendimi çok ayrıcalıklı hissediyorum.
Neden fraktallar özellikle sanatçılar arasında yankı uyandırdı?
M.Ö. 6.yüzyılda güzellik fikri oldukça kısaydı: Her şeyden önce, güzellik, parça ile bütün arasındaki bir denge anlamına geliyordu. Yetenekli sanatçıların böyle düzenlemeler bulması gerekiyordu; her boydan girdabın bir karışımının dengeli görünüşü gibi... Peki, bunun anlamı, her boydan öğelerin doğal -yani fraktal- bir biçimde dağılımı değil miydi? Kimsenin Paris Opera'nın insana uygun boyutlarda olması gerektiğini söylediğini duymadım; devasa bir bina olmasına rağmen. Neden öyle bir duygu uyandırmaz? Çünkü mimar Charles Garnier, tasarımında her ölçekten ayrıntıları bir araya getirmiştir.
Sanatta yankı bulan başka hangi matematiksel örnekler var?
Öklit'in ilk çevirisi Floransa diline yapılmıştı, yani İtalyanca'ya. Peki, İtalya'da Öklit'i dikkate alan ilk insanlar kimlerdi? Matematikçiler değil, mimarlar ve ressamlardı. Ressamlar, örneğin Giotto, 1300 civarında, perspektifi temsil edecek yollar arıyordu. Başaramadılar. Ta ki sonradan Öklit bilinir ve perspektif sağlam bir duruma gelene dek... 1500 civarında Pierre della Francesca'nın çalışmalarında perspektif öylesine güçlü ve ezicidir ki bunu bir resimde ilk kez gördüğümde uzay ile nesne arasında ayrım var gibi gelmişti. Çoğu insan bu resim etkisinin bilim üzerinde büyük olduğunu düşünüyor. Öyle ki, bilim de sonradan referans noktası ile onlara olan olayları ayırmıştır.
Yani sanat ile bilim arasında çift yönlü bir akış mı var?
Ben, sanatı bilimden ayırmanın ve bu faaliyetleri iletişim halinde olmayan parçalara ayırmanın yanlış olduğunu düşünüyorum. Ölümünden kısa süre önce Feynman'a harika bir ziyaret yapmıştım. Konuştuğumuz tek şey şuydu: Nasıl olur da bir insan, bir şeyin resmini görmeden ve onu elinde tutmadan anladığını iddia edebilir? Kendisi bu şekilde ifade edilemeyen herhangi bir düşüncenin eksik ve kavranamaz olduğu fikrinde ısrarcıydı.
Ya siz? Kendi çalışmanızı sanat olarak görüyor musunuz?
Matematik ile sanatı her gün bir araya getiriyorum. Eğer Alman dili özgürce kunstkullanımına bu kadar gönülsüz olmasaydı bu opera aşığı yaşam çabasını Gesamtkunstwerk olarak betimlerdi.
felsefenin, düzensizliğe ve kaosa ilişkin belirli bir yaklaşımın ve ayrıca fiziğin bir parçası olduğunun bilinmesini çok istiyordum. Her seferinde, dergi hakemleri bunlara ilişkin ifadelerimi çıkarmamı istedi. Daha sonra ben türbülans üzerinde çalışmaya geçtim ve editörler "kuşkulu felsefe" olarak aşağıladıkları kısımları çıkarmam için beni zorladı. Onun yerine daha çok formül ve yöntem ayrıntısı istiyorlardı. Her bir olayda, o alanda bir uzmanmışım gibi davranıyordum.
⚛️⚛️⚛️⚛️⚛️⚛️💮💮💮💮💮⚛️⚛️⚛️⚛️⚛️
Fraktal Nedir?
Fraktal; matematikte, çoğunlukla kendine benzeme veya oransal kırılma özelliği gösteren karmaşık geometrik şekillerin ortak adıdır. Fraktallar, klasik, yani Öklid (Euklides) geometrideki kare, daire, küre gibi basit şekillerden çok farklıdır. Bunlar doğadaki, Öklid'çi geometri aracılığıyla tanımlanamayacak pek çok uzamsal açıdan düzensiz olguyu ve düzensiz biçimi tanımlama yeteneğine sahiptir. Fraktal terimi parçalanmış ya da kırılmış anlamına gelen Latince "fractus" sözcüğünden türetilmiştir.
İlk olarak 1975'te Polonya asıllı matematikçi Benoit B. Mandelbrot tarafından ortaya atılan kavram, yalnızca matematik değil fiziksel kimya, fizyoloji ve akışkanlar mekaniği gibi değişik alanlar üzerinde önemli etkiler yaratan yeni bir geometri sisteminin doğmasına yol açmıştır.
Tüm fraktallar kendine benzer ya da en azından tümüyle kendine benzer olmamakla birlikte, çoğu bu özelliği taşır. Kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününe benzer. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza değin sürebilir; öyle ki,her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzer.
Bu fraktal olgusu, kar tanesi ve ağaç kabuğunda kolayca gözlenebilir. Bu tip tüm doğal fraktallar ile matematiksel olarak kendine benzer olan bazıları, stokastik (olasılıksal) yani rastgeledir; bu nedenle ancak istatistiksel olarak ölçeklenirler. Fraktal cisimler, düzensiz biçimli olduklarından ötürü Öklid'çi şekilleri ötelemezler. (Öteleme bakışına sahip bir cisim kendi çevresinde döndürüldüğünde görünümü aynı kalır.)
 Nesne, olay ve olguların bilinmesinde kullanılan ussal ölçüt ise “geometri bilimi”dir. Aritmetik, geometrik biçimlerin açılımı, anlatımıdır. Geometri ve aritmetiğin birliği ise matematiktir. Matematik “nesnel bilimlerin dili”dir.
Nesne, olay ve olguların bilinmesinde kullanılan ussal ölçüt ise “geometri bilimi”dir. Aritmetik, geometrik biçimlerin açılımı, anlatımıdır. Geometri ve aritmetiğin birliği ise matematiktir. Matematik “nesnel bilimlerin dili”dir.
İlk geometrik biçim, usun ilk kavramı “üçgen”dir. Uzayda tek nokta tanımsızdır, iki nokta çizgiyi yani ilişkiyi, üç noktanın ilişkilendirilmesi ise üçgeni yani ilk ussal belirlemeyi, kavramayı verir. Bu nedenle, usun gören (kavrayan) gözü üçgen içinden ışıldar. Her türlü nesnel gerçekliği gören göz, bu gözdür.
Yazar: Metin Bobaroğlu |Kategoriler: Yazılar|











Hiç yorum yok:
Yorum Gönder
Hallo 🙋🏼♀️