Harranlı diferansiyel matematikçi Sâbit Bin Kurra

 

 (836) yılında Harran’da doğdu. İslâm matematiğinin oluşum dönemine katkıda bulunan Harranlı matematikçilerin başında gelmektedir. 

Gençliğinde sarraflık yaptığı nakledilir. Felsefe konularında serbest düşünceleri yüzünden şehrin Sâbiî halkı ile anlaşmazlığa düşünce yargılandı ve görüşlerinden vazgeçmek zorunda kaldı.

Sâbit Süryânîce ve Grekçe bilmekteydi. Kadrî Hâfız Tûkān, İbrânîce de bildiğini söylemektedir (Türâs̱ü’l-ʿArabi’l-ʿilmî, s. 196). Sâbit b. Kurre, Bağdat’ta felsefî ilimlerle uğraşma imkânı buldu. Grek matematikçilerinin eserlerini Arapça’ya çevirerek şerhetti. Matematik ve astronomi alanında eserler yazdı ve hekimlikle meşgul oldu. 

Huneyn b. İshak ile beraber İslâm medeniyetindeki en büyük iki mütercimden biri kabul edilmektedir. Kâtib Çelebi, Sâbit b. Kurre’nin tercümeleri olmasaydı hiç kimsenin hikmete dair Yunanca kitaplardan faydalanamayacağının söylendiğini, nitekim onun tercüme etmediği kitapların öylece kaldığını belirtir (Keşfü’ẓ-ẓunûn, II, 1594).

Sâbit’in İslâm matematiğine katkılarını üç aşamada özetlemek mümkündür. Birinci aşama, Yunan matematiğinin önemli eserlerini Arapça’ya çevirmesi veya daha önce yapılan tercümeleri tashih etmesidir. Sâbit özellikle Archimedes’in matematik alanındaki bütün çalışmalarını Arapça’ya çevirmiştir. Bugün Archimedes’in birçok eserinin Yunanca asılları kayıp olduğundan bu eserlerden Sâbit’in tercümeleri sayesinde haberdar olunmaktadır. Sâbit ayrıca Pergeli Apollonios’un Koni Kesitleri ve Nicomachus’un Aritmetiğe Giriş adlı kitaplarını Arapça’ya çevirmiştir. Öklid, Ptolemy ve Theodosios’un eserlerinden tercümeler yapmış veya yapılan tercümeleri düzeltmiştir.

İkinci aşama, Sâbit’in tercüme ve tashihleri vasıtasıyla Arapça bir matematik dilinin oluşması konusundaki katkılarıdır. Sâbit matematiğe dair eserleri Yunanca veya Süryânîce’den çevirirken güçlü Arapça bilgisi sayesinde bu dillerdeki kavramlara uygun Arapça karşılıklar bulmuştur. Onun belirlediği kavramların bir kısmı daha sonra gelen İslâm matematikçileri tarafından değiştirilirken büyük bir kısmı kullanılmaya devam etmiştir.

Sâbit’in İslâm matematiğine yaptığı üçüncü aşamadaki katkıları ise matematiğin aritmetik (sayılar teorisi), cebir, geometri, koni kesitleri ve trigonometri gibi alanlarında telif ettiği özgün eserlerdir. Bilhassa sayı kavramının pozitif reel sayıları içerecek biçimde genişletilmesi, integral kalkulus, küresel trigonometrinin bazı teoremleri, analitik geometri ve Öklidci olmayan geometri konularındaki çalışmaları kalıcı izler bırakmıştır.

Sayılar Teorisi. Sâbit’in sayılar teorisine en önemli katkılarından biri Yunanlı matematikçi Nicomachos’un Aritmetiğe Giriş adlı eserini tercüme etmesidir (Kitâbü’l-Medḫal ilâ ʿilmi’l-ʿaded elleẕî veḍaʿahû Nîḳūmâḫus, nşr. el-Eb Vilhelm Kutş el-Yesûî, Beyrut 1958). Bu tercümeyle beraber İslâm matematiğine Pisagorcu sayı ve aritmetik anlayışının girmesi yanında eser “theologoumenates aritmetikes” anlamında bir sayı mistisizminin yerleşmesini sağlamıştır. Bu sayı mistisizmi bazı İslâm matematikçileri arasında taraftar bulmakla birlikte bu anlayışı İslâm medeniyetinde sistemli bir şekilde takip eden İhvân-ı Safâ olmuştur (Resâʾilü İḫvâni’ṣ-ṣafâ, nşr. Butrus el-Bustânî, Beyrut, ts., I, 48-113). 

İslâm matematikçileri Pisagorcu aritmetik anlayışını Yunanca aslı ile “ârîtmetîkî” olarak adlandırmış ve bunu “ilmü’l-aded” ismini verdikleri Öklidci geometrik-aritmetik anlayışından ayırmıştır. İbnü’l-Heysem’e göre Pisagorcu aritmetik anlayışının en önemli özelliği tümevarım yöntemini kullanmasıdır. Bu da Pisagorcu aritmetiğin nokta (atom) sayı anlayışına dayanılmasından kaynaklanmaktadır. Öklidci aritmetikte ise tam sayılar doğru çizgilerle temsil edilmekte ve ispatlarda Öklid’in Elementler’indeki geometrik burhan anlayışı esas alınmaktadır. 

Sâbit’in Maḳāle fi’stiḫrâci’l-aʿdâdi’l-müteḥâbbe (Kitâbü’l-Aʿdâdi’l-müteḥâbbe, nşr. Ahmed Selîm Saîdân, Amman 1977) adlı eserinde yer alan sayılar teorisindeki ikinci ve özgün katkısı Öklidci aritmetik anlayışından hareket ederek tam, nâkıs ve zâit sayı çeşitlerinin özelliklerini incelemesi, tam bölen parçalar üzerinde çalışması ve bu iki çalışmanın sonucundan hareket ederek dost sayılar için genel bir formül ortaya koymasıdır. Bu araştırmaları esnasında asal sayıların, sayıların özelliklerini incelemedeki rolüne işaret etmesi oldukça önemli sonuçlar doğurmuştur.

Sâbit’in verdiği formül şu şekilde özetlenebilir: Eğer 𝑛∈𝑁$n\in N$’nin tam bölen parçaları veya fiili bölenleri, n sayısının kendisi hariç σ_o(n) ile gösterilirse bölenlerin toplamı σ(n) = σ_o(n) + n olarak yazılabilir. Bu durumda 𝑛∈𝑁$n\in N$’i, eğer σ_o(n) > n ise zâit, σ_o(n) < n ise nâkıs ve σ_o(n) = n ise tam olarak isimlendirilir. Bu şartlarda 𝑚,𝑛∈𝑁$m,n\in N$’nin dost sayı olması demek, σ_o(m) = n ve σ_o(n) = m olması demektir. Sâbit’in bu şartı sağlayan dost sayı çifti formülü ise şöyledir: P_n= 3.2ⁿ - 1 ve q_n= 9.2^2n-1-1 olduğunu var sayalım; eğer q_n, P_n ve P_n-1 asal sayı iseler m= 2ⁿP_n-1P_n ve n= 2ⁿq_ndost sayı olur; burada m zâit sayı, n ise nâkıs sayıdır.

Sâbit b. Kurre’nin araştırmaları tercümeler vasıtasıyla Avrupa’ya ulaşmış, Fermat ve Descartes üzerinde etkili olmuştur. Daha sonra Euler, Sâbit’in dost sayılar için geliştirdiği formülü modern Batı Avrupa matematiğinin verdiği yeni imkânlarla genelleştirmiştir (Rüşdî Râşid, s. 299-346; Brentjes, IV/11 [1988], s. 467-483, T trc. Melek Dosay, s. 485-500). 

Geometri. III. (IX.) yüzyılda trigonometrik hesaplamalarda Yunanlılar’ın kullandığı kirişler anlayışı bırakılarak sinüslere dayalı bir trigonometrinin temelleri atılmakla birlikte bu adımı ilk atan kişiyi tesbit etmek oldukça zordur. Ancak en azından Sâbit’in Menelaus problemini ilk çözen kişi olduğunu gösteren deliller mevcuttur. Batlamyus, küresel astronomi problemlerini çözmek için Menelaus’un tam küresel dörtgen teoremini kullanmaktaydı. Sâbit, Risâle fi’ş-şekli’l-ḳaṭṭâʿ adlı eserinde konuyu yeniden ele almış ve Menelaus’un teoreminin mükemmel bir ispatını vermiştir. 

BİBLİYOGRAFYA

İbn Cülcül, Ṭabaḳātü’l-eṭıbbâʾ (nşr. Fuâd Seyyid), Beyrut 1405/1985, s. 75.

İbnü’n-Nedîm, el-Fihrist (nşr. Nâhid Abbas Osman), Devha 1985, s. 548-550.

Bîrûnî, Taḥdîdü nihâyâti’l-emâkin (nşr. Muhammed b. Tâvît et-Tancî), Ankara 1962, s. 27, 72, 203.

Sâid el-Endelüsî, Ṭabaḳātü’l-ümem, s. 41, 42.

İbn Ebû Usaybia, ʿUyûnü’l-enbâʾ, s. 295-300, 307.

İbnü’l-Kıftî, İḫbârü’l-ʿulemâʾ, s. 42-43, 80-85, 130-133, 300-304.

İbn Hallikân, Vefeyât, I, 313-315.

Taşköprizâde, Miftâḥu’s-saʿâde, I, 270, 374.

Keşfü’ẓ-ẓunûn, II, 1594.

Suter, Die Mathematiker, s. 34-38, 51-52, 53-54.

Sâlih Zeki, Âsâr-ı Bâkıye, İstanbul 1329, I, 157-159.

D. E. Smith, History of Mathematics, New York 1953, II, 685.

Sarton, Introduction, I, 599-600, 631-632, 641.

Kadrî Hâfız Tûkān, Türâs̱ü’l-ʿArabi’l-ʿilmî fi’r-riyâżiyyât ve’l-felek, Beyrut, ts. (Dârü’ş-şark), s. 195-205.

Sezgin, GAS, III, 260-263, 377; IV, 163-170, 193-195; V, 264-272, 291, 292-295, 402; VI, 151-152, 163-170, 269-270, 274-275, 329-339; VII, 151-152, 268-270, 404-405.

B. A. Rosenfeld – A. T. Grigorian, “Thabit b. Qurra”, DSB, XIII, 288-295.

Aydın Sayılı, Abdülhamid İbn Türk’ün Katışık Denklemlerde Mantıkî Zaruretler Adlı Yazısı ve Zamanın Cebri: Logical Necessities in Mixed Equations by Abd al Hamid Ibn Turk and the Algebra of His Time, Ankara 1985, s. 74.

Naẓariyyetü’l-mütevâziyyât fi’l-hendeseti’l-İslâmiyye(nşr. Halîl Çâvîş), Tunus 1988, s. 58-84.

B. A. Rosenfeld – A. P. Youschkevitch, Naẓariyyetü’l-ḫuṭûṭi’l-mütevâziyye fi’l-meṣâdiri’l-ʿArabiyye (trc. Sâmî Şelhûb – Kemâl Necîb Abdurrahman), Halep 1989, s. 58-74.

Rüşdî Râşid, Târîḫu’r-riyâżiyyâti’l-ʿArabiyye beyne’l-cebr ve’l-ḥisâb (trc. Hüseyin Zeynüddin), Beyrut 1989, s. 279, 299-346.

a.mlf. – R. Morelon, “Thābit b. Ḳurra”, EI² (İng.), X, 428-429.

Ebü’l-Kāsım Kurbânî, Zindegînâme-i Riyâżîdânân-ı Devre-i İslâmî, Tahran 1365 hş., s. 204-210.

Victor J. Katz, A History of Mathematics: An Introduction, New York 1993, s. 233-234, 252-253.

Ilias Fernini, A Bibliography of Scholars in Medieval Islam: 150-1000 A.H. (750-1600 A.D.), Abu Dhabi 1998, s. 424-435.

B. A. Rosenfeld – Ekmeleddin İhsanoğlu, Mathematicians, Astronomers and Other Scholars of Islamic Civilization and Their Works (7^th-19^th c.), Istanbul 2003, s. 48-56.

S. Brentjes, “The First Perfect Numbers and Three Types of Amicable Numbers in a Manuscript on Elementary Number Theory by Ibn Fallûs”, Erdem, IV/11, Ankara 1988, s. 467-483 (Türkçe tercümesi: Melek Dosay, s. 485-500).

J. Ruska, “Sâbit”, İA, X, 14-15.

Sabit bin Kurra, yaşadığı döneminin en büyük matematikçilerinden biri olarak kabul edilmektedir. Tıpkı ünlü astronom Battani gibi günümüz Urfa ilinin sınırları içinde bulunan Harran’da dünyaya gelmiştir. Doğum yılı 826 ya da 836 olarak verilmekle birlikte, ünlü İslam filozofu Kindi ile aynı dönemde yaşamış olan Sabit bin Kurra, Sabii dinine mensup bir ilim insanıydı.

Süryanice. İşte Sabit bin Kurra’nın ana dili de Süryanice’ydi. Fakat o hem Yunanca hem de Arapça biliyordu. Bu özelliği sayesinde Sabit bin Kurra, Bağdat’taki tercüme faaliyetlerine dahil olma fırsatına sahip olacaktı.

SABİT BİN KURRA’NIN MATEMATİĞE KATKILARI

Sabit bin Kurra matematik alanında Öklid, Arşimet, Apollonius gibi birçok antik Yunan matematikçinin çalışmalarını tercüme etti ya da yeniden düzenledi. Ayrıca Batlamyus‘un Almagest eseri üzerine de bir yorum yazmıştı.

Maqāla fī Istikhrāj al-A’dād al-Mutahābba (Dost Sayıların Belirlenmesi Üzerine) isimli bir kitap yazan Sabit bin Kurra, burada “Dost Sayılar” olarak bilinen sayıların varlığından bahseder. 

Herhangi iki sayı, birbirlerinin pozitif bölenlerinin toplamına eşit oluyorsa o sayılar dost sayılardır. Örneğin 220 ve 284 sayısını ele alalım. 220’nin bölenleri  1, 2, 4, 5, 10, 11, 20, 22, 44, 55 ve 110’dur. Bu sayıları toplarsak 284 sayısını elde ederiz. 284 sayısının ise pozitif bölenleri 1, 2, 4, 71 ve 142’dir. Bu sayıların toplamı ise 220 eder. O zaman 220 ve 284 dost sayılardır.

Bağdaşık Sayılar olarak da adlandırılan dost sayıların ilk çiftini, Milattan önce 6.yüzyılda yaşamış olan ünlü matematikçi ve filozof Pisagorkeşfetmiştir. Kitāb fī Ta’līf al-Nisab isimli kitabında ise bileşik oranlar teorisini ele alan Sabit bin Kurra, yaptığı bu çalışmayla reel sayılar kavramına ve diferansiyel denklemlerin keşfine giden yolu döşemiştir diyebiliriz.

Sabit bin Kurra’nın matematiksel zekasını gösterdiği bir diğer alan ise Öklid’in beşinci postulatını kanıtlamak üzerinedir. Bu problemi ise iki yazısında inceler: Maqāla fī Burhān al-Musādara al-Mašhūra min Uqlīdis (Öklid’in Meşhur Postulatının Kanıtı) ve Maqāla fī anna al–khattayn Idhā Ukhrijā ‘alā Zāwiyatayn Aqal min Qā’imatayn Iltaqayā (İki Dik Açıdan Daha Az Açıyla Çizilen İki Doğru Parçasının Kesişmesi). Problemi iki biçimde ele alan Sabit bin Kurra ilkinde, iki doğru parçasını kesen üçüncü doğru parçası modeliyle ilgili birtakım belirsiz ifadelerde bulunur. İkinci olarak ele alışında ise Öklid’in geometrideki hareket kullanımını yasaklayan yaklaşımını eleştirerek “hareket” kavramı üzerinde durur. Sabit bin Kurra’nın bu sonuçları daha sonraları İbn-ül Heysem, Ömer Hayyam ve Nasirüddin Tusi gibi bilim insanları tarafından geliştirilecek ve nihayetinde Öklid-dışı geometrinin keşfini mümkün kılacaktır.

Görsel: Sabit bin Kurra’nın, Apollonius’un Konik adlı eserine yaptığı Arapça tercümenin bir sayfası görülüyor.

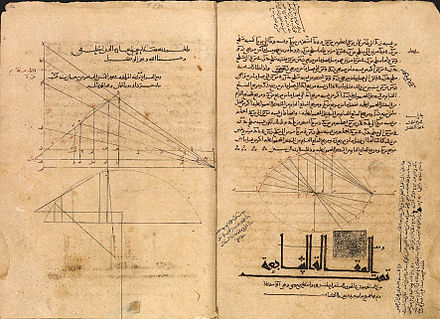
Sabit bin Kurra, Kitāb fī Misāhat Qat’ al-Makhrūt alladhī Yusammā al-Mukāfi’ isimli kitabında bir parabol kesitinin alanını hesaplar. Matematik tarihçileri ise Arşimet‘in kullandığı tüketme yönteminden farklı olan bu hesabın integral yöntemine eşit olduğunu söylüyor. Aynı zamanda M.Ö 4.yüzyılda yaşamış ünlü Yunan matematikçisi Eudoxus’un da Arşimet’e benzer bir tüketme yöntemi kullanmış olduğunu söyleyelim. Sabit bin Kurra’nın matematiğe yaptığı katkılardan bir diğeri ise Harezmi‘nin bulduğu cebir yöntemini geometriye uygulamış olmasıydı.

Bilim Tarihçisi R.Morelon ise Sabit bin Kurra’dan ve çalışmalarının öneminden şöyle bahsediyor:

9.yüzyıl Bağdatı’nda gerçekleşen bilimsel aktiviteler bağlamında yazılan bu kadar çok eseri göz önünde bulundurduğumuzda, Sabit bin Kurra’nın astronominin bir bilim haline gelmesinde oynadığı rol çok büyüktür.

KAYNAKLAR:

1- Thabit Ibn Qurra, Al-S?abi? Al-H?arrani .”Complete Dictionary of Scientific Biography. Encyclopedia.com. <https://www.encyclopedia.com>.(Erişim:30.05.2021)

2- Palmeri J. (2007). “Thābit ibn Qurra”. Springer. https://islamsci.mcgill.ca/RASI/BEA/Thabit_ibn_Qurra_BEA.htm (Erişim:30.05.2021)

3- Muslim Heritage, “Thabit ibn Qurra”. https://muslimheritage.com/thabit-ibn-qurra/ (Erişim: 29.05.2021)

4- Wikipedia, “Thābit ibn Qurra”. https://en.wikipedia.org/wiki/Th%C4%81bit_ibn_Qurra(Erişim: 30.05.2021)

5- Famous Scientists, “Thabit ibn Qurra”. https://www.famousscientists.org/thabit-ibn-qurra/(Erişim: 29.05.2021)

6- J.J O’Connor, E.F Robertson (1999). “Al-Sabi Thabit ibn Qurra al-Harrani”. Mactutor History Of Mathematics. https://mathshistory.st-andrews.ac.uk/Biographies/Thabit/#reference-20 (Erişim: 30.05.2021)

7- Wikipedia, “Trepidiation”. https://en.wikipedia.org/wiki/Trepidation (Erişim: 30.05.2021)

8- Dönmez, A. (2010). “Sabit bin Kurra’nın İkinci Derece Denklemlerinin Geometrik Çözümleri“. Anadolu Bil Meslek Yüksekokulu Dergisi. Cilt(18). 12-23. (Erişim: 30.05.2021)