Duyduğunuz sesler – kulaklarınızın algıladığı en minimal ve maksimal sesler de dahil doğada titreşimlerin bir ürünü olarak dalgalanan ses dalgalarının kulaklarımızda bulunan salyangozda aktif hale gelmesi ile sürece girdikten sonra beyne giden sinyallerden sonra da algılama ile bitmektedir.

8. kranial sinir olan vestibüler sinir, işitme ve denge duyusunda etkili olan sinirdir.

Koklear sinir. Koklear sinir ( işitsel sinir veya akustik sinir olarak da bilinir)

İç kulakta kokleanın arkasında bulunan işitme siniri, yarım daire kanallarına ve vestibüler organa bağlanır.Duyma sinirleri çevresel sinir sistemindeki duyu reseptörlerinden gelen afferent sinir liflerinin kablo benzeri demetleridir.

İç Kulak

İç kulak, kulak yapısının en önemli dokularının bulunduğu alandır. Bu dokular;

Dalız
Kulak salyangozu
Yarım daire kanalları olmaktadır.

Bu dokular, işitilen sesin sinirler yardımıyla beyne iletilmesini sağlamakta ve beynin o sesi anlamasına yardımcı olmaktadır. İşitme sinirleri nerede bulunursorusunun cevabı ise iç kulaktır.

Dış ve orta kulak bölgelerinde kulak yapısı korunmakta ve iç kulak ile köprü kurulmaktadır. Bu sayede kulak dengesi sağlanmaktadır. İç kulakta bulunan sinirler, algılanan sesi beyne iletir ve beyin iletilen sesi çok hızlı bir şekilde çözümleyerek duyma sürecini tamamlamaktadır. Ancak bu dokularda herhangi bir sorun olması durumunda sesler daha az anlaşılmakta ve ses algılama sorunları meydana gelmektedir. İşitme siniri hasarı birkaç faktörden kaynaklanabilir. Örneğin, travma, enfeksiyon (menenjit gibi) veya yüksek doz antibiyotikler veya belirli kanser ilaçları gibi ototoksik ilaçların kullanımından sonra işitme sinirlerinde hasar meydana gelebilir.

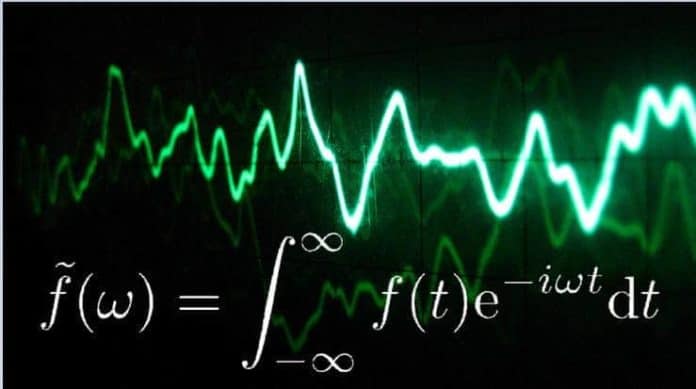
Joseph Fourier “Bir ses dalgasının ifadesi veya zamana bağlı olarak değişen herhangi bir sinyalin, oluşturan sinüs dalgalarının toplamı, o sinyalin Fourier dönüşümü olarak nitelendirilecektir.” Bu çok kesin bir bilgiydi ve zamanla da doğruluğu kabul edilir.

Holonomik beyin teorisi, bilincin beyin hücreleri içinde veya arasında kuantum etkileriyle oluştuğu fikrini araştıran bir sinirbilim dalıdır . Holonomik, hem spektral hem de ^uzay -zaman koordinatlarıyla tanımlanan bir Hilbert faz uzayındaki temsilleri ifade eder.

Fourier dönüşümü

Matematikte , Fourier dönüşümü ( FT ), girdi olarak bir fonksiyon alıp ardından orijinal fonksiyonda bulunan çeşitli frekansların derecesini tanımlayan başka bir fonksiyon çıkaran bir integral dönüşümdür.

Fourier dönüşümü , bir müzik akorunun sesini , onu oluşturan perdelerin yoğunluklarına ayrıştırmaya benzer.

Zaman alanında yerelleştirilmiş fonksiyonlar, frekans alanında yayılmış Fourier dönüşümlerine sahiptir ve bunun tersi de geçerlidir; bu, belirsizlik ilkesi olarak bilinen bir olgudur . Bu ilke için kritik durum, olasılık teorisi ve istatistikte ve normal dağılımgösteren fiziksel olguların (örneğin, difüzyon) incelenmesinde önemli bir öneme sahip olan Gauss fonksiyonudur .

Joseph Fourier, ısı transferi çalışmasında , Gauss fonksiyonlarının ısı denkleminin çözümleri olarak göründüğü sinüs ve kosinüs dönüşümlerini ( modern Fourier dönüşümünün sanal ve gerçek bileşenlerine karşılık gelir ) tanıttı .

Fourier dönüşümü ayrıca Öklid uzayında birden fazla değişkenin fonksiyonlarına genelleştirilebilir ve 3 boyutlu 'konum uzayı'nın bir fonksiyonunu 3 boyutlumomentumun bir fonksiyonuna (veya uzay ve zamanın bir fonksiyonunu 4-momentumunbir fonksiyonuna ) gönderir. Bu fikir, uzaysal Fourier dönüşümünü dalgaların incelenmesinde ve dalga çözümlerini konum veya momentumun ve bazen her ikisinin de fonksiyonları olarak gösterebilmenin önemli olduğu kuantum mekaniğinde çok doğal hale getirir .

Karmaşık sinüzoidler

Kırmızı sinüzoid , tepe genliği (1), tepe-tepe (2), RMS(3) ve dalga boyu (4) ile tanımlanabilir . Kırmızı ve mavi sinüzoidlerin faz farkı

θ'dir

Birimler:

Frekans değişkeni, orijinal fonksiyonun etki alanının birimlerine ters birimlere sahip olmalıdır (genellikle şu şekilde adlandırılır: $t$ veya $x$ ). Örneğin, eğer $t$ saniyelerle ölçülür, $\xi$ saniye başına döngü veya hertz cinsinden olmalıdır.

Zaman ölçeği birimler halindeyse $2\pi$ saniyeler sonra başka bir Yunan harfi $\omega$ genellikle açısal frekansı temsil etmek için kullanılır (burada $\omega =2\pi \xi$ ) radyan /saniye cinsinden . Kullanıyorsanız $x$ uzunluk birimleri için, o zaman $\xi$ ters uzunlukta olmalıdır, örneğin, wavenumbers . Yani, gerçek çizginin iki versiyonu vardır: biri aralığıdır $t$ ve birimlerle ölçüldü $t,$ ve diğeri ise aralığıdır $\xi$ ve birimlerin ters birimlerinde ölçüldü $t.$ Gerçek doğrunun bu iki farklı versiyonu birbirleriyle eşitlenemez. Bu nedenle, Fourier dönüşümü bir fonksiyon uzayından farklı bir fonksiyon uzayına gider: farklı bir tanım alanına sahip fonksiyonlar.

Genel olarak, $\xi$ her zaman etki alanının uzayında doğrusal bir form olarak alınmalıdır , yani ikinci gerçek doğru, birinci gerçek doğrunun ikili uzayıdır . Daha resmi bir açıklama ve daha fazla ayrıntı için doğrusal cebir hakkındaki makaleye bakın. Bu bakış açısı , Fourier serisi durumu da dahil olmak üzere, Fourier dönüşümünün genel simetri gruplarına genelleştirilmesinde önemli hale gelir .

Zaman ölçeklemesi:

$f(ax)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\frac {1}{|a|}}{\widehat {f}}\left({\frac {\xi }{a}}\right);\quad \ a\neq 0$ Dava $a=-1$ zamanın tersine çevrilmesi özelliğine yol açar : $f(-x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\widehat {f}}(-\xi )$

\scriptstyle f(t)

\scriptstyle {\widehat {f}}(\omega )

\scriptstyle g(t)

\scriptstyle {\widehat {g}}(\omega )

\scriptstyle t

\scriptstyle \omega

\scriptstyle t

\scriptstyle \omega

Çift simetrili gerçek değerli bir fonksiyonun dönüşümü

(f(t)=f_{RE})

aynı zamanda eşit simetrili gerçek değerli bir fonksiyondur

({\hat {f}}_{RE}).

Zaman kayması,

(g(t)=g_{RE}+g_{RO}),

hayali bir bileşen oluşturur,

i\cdot {\hat {g}}_{IO}.

(bkz. § Simetri .

Simetri

Karmaşık bir fonksiyonun gerçek ve sanal kısımları çift ve tek kısımlarınaayrıştırıldığında , aşağıda RE, RO, IE ve IO alt simgeleriyle gösterilen dört bileşen vardır.

Düzgün süreklilik ve Riemann–Lebesgue lemması

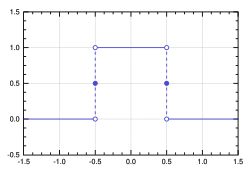
Fourier dönüşümü bazı durumlarda integrallenemeyen fonksiyonlar için tanımlanabilir, ancak integrallenebilen fonksiyonların Fourier dönüşümlerinin birkaç güçlü özelliği vardır.

Evrişim teoremi:

Fourier dönüşümü, fonksiyonların evrişimi ve çarpımı arasında geçiş yapar. Eğer $f (x)$ ve $g (x)$ sırasıyla Fourier dönüşümleri $f̂ (ξ)$ ve $ĝ (ξ)$ olan integrallenebilir fonksiyonlarsa , o zaman evrişimin Fourier dönüşümü, Fourier dönüşümleri $f̂ (ξ)$ ve $ĝ (ξ)$ 'nin çarpımı ile verilir (Fourier dönüşümünün tanımı için kullanılan diğer kurallar altında sabit bir faktör ortaya çıkabilir).

Alternatifler:

Sinyal işleme terimlerinde , bir fonksiyon (zamanın) mükemmel zaman çözünürlüğünesahip , ancak frekans bilgisi olmayan bir sinyalin gösterimidir; Fourier dönüşümü ise mükemmel frekans çözünürlüğüne sahiptir , ancak zaman bilgisi yoktur: Fourier dönüşümünün bir noktadaki büyüklüğü ne kadar frekans içeriği olduğunu gösterir, ancak konum yalnızca faz tarafından verilir (bir noktadaki Fourier dönüşümünün argümanı) ve duran dalgalar zaman içinde yerelleştirilmemiştir - bir sinüs dalgası bozulmadan sonsuza kadar devam eder.

Bu, özellikle geçici sinyaller veya sonlu boyuttaki herhangi bir sinyal olmak üzere zaman içinde yerelleştirilmiş sinyalleri analiz etmede Fourier dönüşümünün kullanışlılığını sınırlar .

Fourier dönüşümüne alternatif olarak, zaman-frekans analizinde , sinyalleri biraz zaman bilgisi ve biraz frekans bilgisi içeren bir biçimde temsil etmek için zaman-frekans dönüşümleri veya zaman-frekans dağılımları kullanılır; belirsizlik ilkesine göre, bunlar arasında bir takas vardır. Bunlar, kısa süreliFourier dönüşümü , kesirli Fourier dönüşümü , Senkronize Sıkıştırmalı Fourier dönüşümü gibi Fourier dönüşümünün genellemeleri veya dalgacık dönüşümleri ve chirplet dönüşümlerinde olduğu gibi sinyalleri temsil etmek için diğer fonksiyonlar olabilir; (sürekli) Fourier dönüşümünün dalgacık analoğu ise sürekli dalgacık dönüşümüdür.

Fourier dönüşümünün +3 Hz'deki mutlak değeri 0,5'tir, bu nispeten büyüktür. -3 Hz'deki Fourier dönüşümüne eklendiğinde (ki bu özdeştir çünkü gerçek bir sinyalle başladık), 3 Hz frekans bileşeninin genliğinin 1 olduğunu buluruz.

Güçlü 3 Hz bileşeni olan orijinal fonksiyon. Fourier dönüşümünün +3 Hz'deki integrandının gerçek ve sanal kısımları.

Uygulamalar:

Bir alanda (zaman veya frekans) gerçekleştirilen doğrusal işlemlerin diğer alanda karşılık gelen işlemleri vardır ve bunlar bazen gerçekleştirilmesi daha kolaydır. Zaman alanında farklılaştırma işlemi , frekansla çarpmaya karşılık gelir, bu nedenle bazı diferansiyel denklemlerinfrekans alanında analiz edilmesi daha kolaydır. Ayrıca, zaman alanındaki evrişim , frekans alanındaki sıradan çarpmaya karşılık gelir (bkz. Evrişim teoremi ). İstenen işlemleri gerçekleştirdikten sonra, sonucun zaman alanına geri dönüştürülmesi yapılabilir. Harmonik analiz , frekans ve zaman alanları arasındaki ilişkinin sistematik çalışmasıdır ve bir veya diğerinde "daha basit" olan işlev veya işlem türlerini içerir ve modern matematiğin birçok alanıyla derin bağlantıları vardır.

Kuantum mekaniği:

Fourier dönüşümü kuantum mekaniğinde en az iki farklı şekilde faydalıdır . Öncelikle, kuantum mekaniğinin temel kavramsal yapısı, Heisenberg belirsizlik ilkesi ile birbirine bağlanan tamamlayıcı değişken çiftlerinin varlığını varsayar . Örneğin, bir boyutta, diyelim ki bir parçacığın uzaysal değişkeni $q , yalnızca parçacığın momentumu$ $p$ hakkında bilgi kaybetme pahasına kuantum mekanik " konum operatörü " tarafından ölçülebilir.

Bu nedenle, parçacığın fiziksel durumu, q'nun "dalga fonksiyonu" adı verilen bir fonksiyonuyla $veya$ $p'nin$ bir fonksiyonuyla tanımlanabilir, ancak her iki değişkenin bir fonksiyonuyla tanımlanamaz. $p değişkenine$ $q'nun$ eşlenik değişkeni denir.

Klasik mekanikte, bir parçacığın fiziksel durumu (açıklamanın basitleştirilmesi için tek boyutta mevcuttur) hem $p'ye$ hem de $q'ya$ aynı anda kesin değerler atayarak elde edilirdi . Bu nedenle, tüm olası fiziksel durumların kümesi, $p$ ekseni ve $q$ ekseni olan iki boyutlu gerçek vektör uzayıdır ve buna faz uzayı denir .

$Buna karşılık, kuantum mekaniği bu uzayın polarizasyonunu, örneğin yalnızca q$ ekseni gibi boyutun yarısının bir alt uzayını seçmesi anlamında seçer , ancak yalnızca noktaları dikkate almak yerine, bu eksendeki tüm karmaşık değerli "dalga fonksiyonları" kümesini alır. Bununla birlikte, $p$ eksenini seçmek eşit derecede geçerli bir polarizasyondur ve parçacığın olası fiziksel durumlarının kümesinin farklı bir temsilini verir. Dalga fonksiyonunun her iki temsili de bir Fourier dönüşümü ile ilişkilidir, böylece $\phi (p)=\int dq\,\psi (q)e^{-ipq/h},$ veya eşdeğer olarak, $\psi (q)=\int dp\,\phi (p)e^{ipq/h}.$

Fiziksel olarak gerçekleştirilebilir durumlar $L 2 '$ dir ve bu nedenle Plancherel teoremine göre , bunların Fourier dönüşümleri de $L 2 '$ dir . ( $q'nun$ mesafe birimlerinde ve $p'nin$ momentum birimlerinde olduğuna dikkat edin, üsteki Planck sabitinin varlığı üsteli boyutsuz yapar , öyle de olması gerekir.)

Bu nedenle, Fourier dönüşümü parçacığın durumunu bir konum dalga fonksiyonuyla temsil etmenin bir yolundan, parçacığın durumunu bir momentum dalga fonksiyonuyla temsil etmenin başka bir yoluna geçmek için kullanılabilir.

Sonsuz sayıda farklı polarizasyon mümkündür ve hepsi eşit derecede geçerlidir. Fourier dönüşümüyle durumları bir temsilden diğerine dönüştürebilmek yalnızca kullanışlı olmakla kalmaz, aynı zamanda Heisenberg belirsizlik ilkesinin altında yatan nedendir .

Fourier dönüşümünün hem kuantum mekaniğinde hem de kuantum alan teorisinde diğer kullanımı, uygulanabilir dalga denklemini çözmektir. Relativistik olmayan kuantum mekaniğinde, dış kuvvetlere tabi olmayan, tek boyutlu, zamanla değişen bir dalga fonksiyonu için Schrödinger denklemi , $-{\frac {\partial ^{2}}{\partial x^{2}}}\psi (x,t)=i{\frac {h}{2\pi }}{\frac {\partial }{\partial t}}\psi (x,t).$

$Bu, sanal birim i'nin$ varlığı dışında ısı denklemiyle aynıdır . Bu denklemi çözmek için Fourier yöntemleri kullanılabilir.

$Potansiyel enerji fonksiyonu V (x)$ ile verilen bir potansiyelin varlığında denklem şu hale gelir: $-{\frac {\partial ^{2}}{\partial x^{2}}}\psi (x,t)+V(x)\psi (x,t)=i{\frac {h}{2\pi }}{\frac {\partial }{\partial t}}\psi (x,t).$

Yukarıda bahsettiğimiz "temel çözümler", parçacığın sözde "durağan durumları"dır ve yukarıda açıklandığı gibi Fourier algoritması, $t$ $= 0$ için değerleri verildiğinde $ψ'nin$ gelecekteki evriminin sınır değer problemini çözmek için hala kullanılabilir.

Bu yaklaşımların hiçbiri kuantum mekaniğinde pek pratik bir işe yaramaz. Sınır değer problemleri ve dalga fonksiyonunun zaman evrimi pek pratik bir ilgiye sahip değildir: en önemli olan durağan durumlardır.

Relativistik kuantum mekaniğinde, Schrödinger denklemi klasik fizikte olduğu gibi bir dalga denklemi haline gelir, ancak karmaşık değerli dalgalar dikkate alınır. Diğer parçacıklar veya alanlarla etkileşimlerin yokluğunda basit bir örnek, bu sefer boyutsuz birimlerde olan serbest tek boyutlu Klein–Gordon–Schrödinger–Fock denklemidir, $\left({\frac {\partial ^{2}}{\partial x^{2}}}+1\right)\psi (x,t)={\frac {\partial ^{2}}{\partial t^{2}}}\psi (x,t).$

Bu, matematiksel bakış açısından, yukarıda çözülen klasik fiziğin dalga denklemiyle aynıdır (ancak yöntemlerde hiçbir fark yaratmayan karmaşık değerli bir dalga ile). Bu, kuantum alan teorisinde büyük bir kullanımdır: bir dalganın her ayrı Fourier bileşeni ayrı bir harmonik osilatör olarak ele alınabilir ve sonra kuantize edilebilir, bu "ikinci kuantizasyon" olarak bilinen bir prosedürdür. Fourier yöntemleri önemsiz olmayan etkileşimlerle başa çıkmak için de uyarlanmıştır.

Son olarak, kuantum harmonik osilatörünsayı operatörü , örneğin Mehler çekirdeğiaracılığıyla , Fourier dönüşümünün üreteciolarak yorumlanabilir ${\mathcal {F}}$ [

Xxx

„ Kim de bir can kurtarırsa bütün insanların hayatını kurtarmış gibi olur.” -Mâide,32

2 Mayıs 2025 Cuma

Joseph Fourier; (Fourier dönüşümü)